Baptiste Coulmont

L’Insee a rendu public, sur le site Statistiques locales, le nombre et la fréquence des procurations en 2022, au niveau communal.
Voici donc une carte montrant, pour la France métropolitaine, le « taux de procurations » en 2022 :

La procuration est plus fréquente dans l’Ouest parisien (des villes riches comme Neuilly ou Versailles), dans les métropoles régionales (Nantes, Rennes, Lyon), dans les zones de montagne (où l’on trouve par ailleurs des inscrits qui n’y résident pas), la Corse mais aussi les villes et villages du littoral de la Manche et de l’Atlantique (zones de résidences secondaires).

Il y a, en 2022, environ 502 000 élus dans les différents conseils municipaux en France. Le répertoire national des élus est téléchargeable sur data.gouv.fr. Les prénoms les plus fréquents sont Jean, Marie, Philippe, Michel…
Mais ces prénoms sont aussi fréquents dans la population française non élue. Quels sont donc les prénoms qui sont sur-représentés chez les élus ?

Voici le raisonnement que j’ai suivi : j’ai comparé les prénoms des élus avec les prénoms des personnes nées en France, à partir du Fichier des prénoms, de l’Insee. Je vais présenter les résultats sous la forme d’un graphique qui compare la distribution des prénoms dans le Répertoire national des élus avec la distribution du Fichier des prénoms. Voici un graphique explicatif :
 

Vous remarquerez que les échelles sont logarithmiques.

Première comparaison

Je commence par comparer la population des élus et élues avec la population née en France depuis 1900 à partir du Fichier des prénoms. S’il y a 1,2% des naissances qui sont des naissances de bébés prénommés Zygloub et qu’il y a 2,4% de Zygloub parmi les élus, alors Zygloub est 2 fois plus présent chez les élus que ce qui est attendu (2 = 2,4 / 1,2).

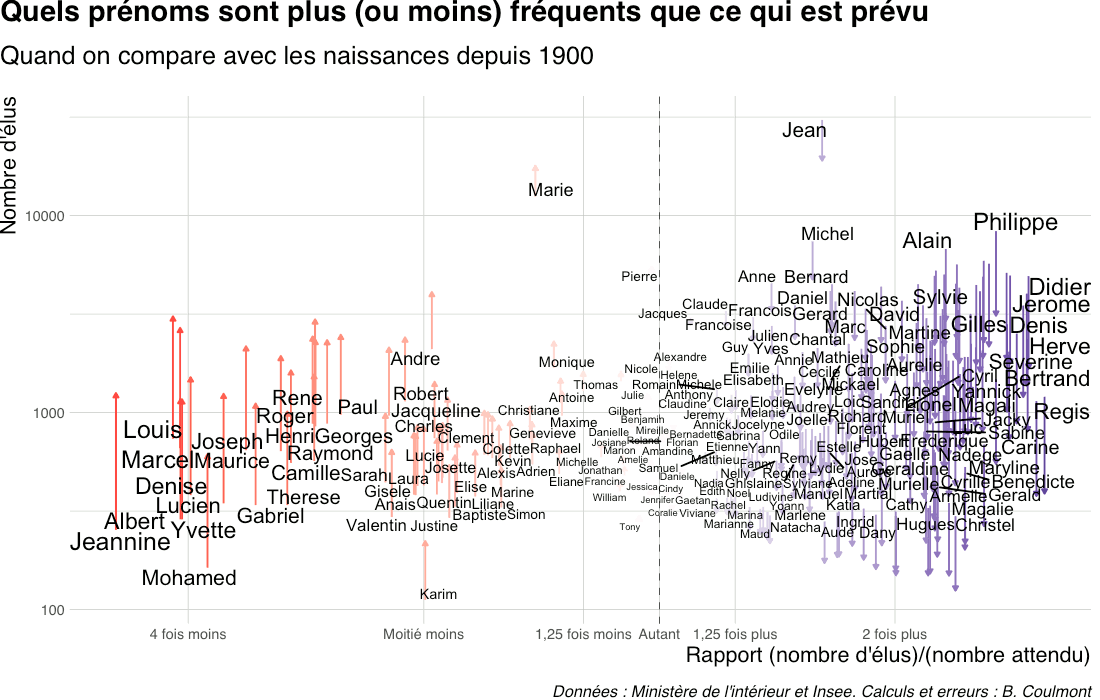
Apparemment, il y a “trop” de Didier et de Régis parmi les élus, et “pas assez” de Jeannine, de Mohamed et de Thérèse. Quatre fois moins de Louis qu’attendu, et trois fois plus d’Hervé.
Mais on a tout de suite un problème : la population des élus municipaux compte moins de femmes que la population française, ce qui va se refléter sur la position des prénoms sur ce graphique. Je vais donc faire une deuxième comparaison, en tenant compte de la part des femmes parmi les élu·e·s.

Deuxième comparaison

Cela ne change pas grand chose, mais on voit des prénoms comme Justine ou Marie se rapprocher d’un rapport d’égalité :
 

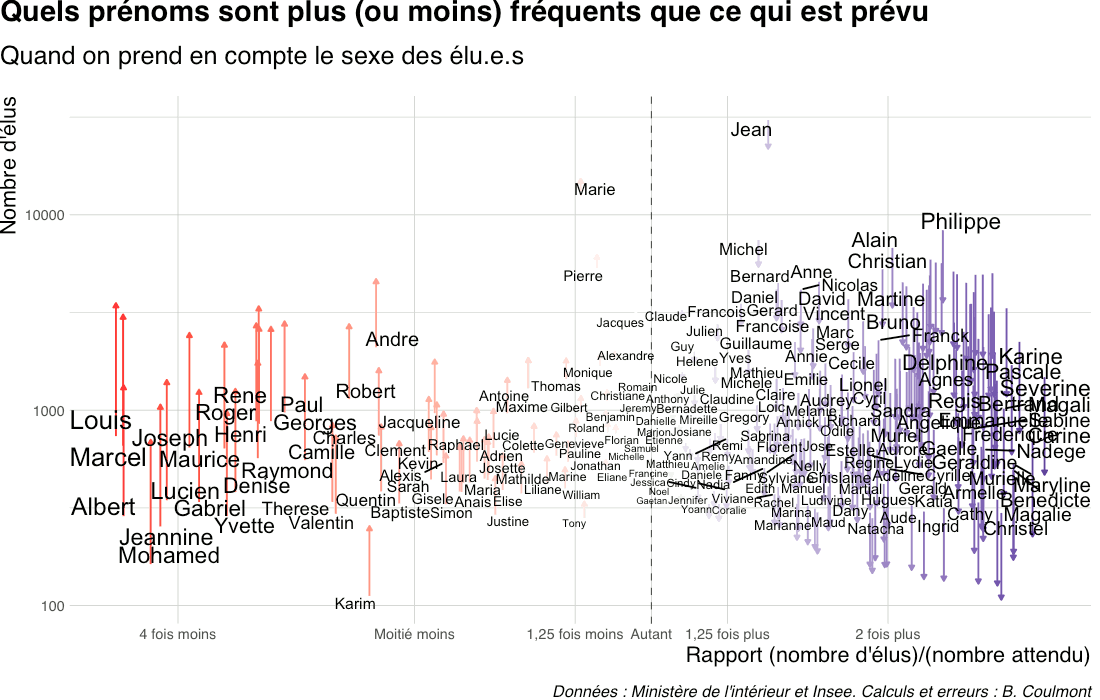
Et de l’autre côté du graphique, les prénoms masculins sur-représentés apparaissent moins sur-représentés (étant donné que les hommes constituent la majorité des élus).

Troisième comparaison

On peut aller plus loin : les élus municipaux sont principalement des élus de toutes petites communes. Et à Paris, par exemple, il y a peu d’élus municipaux par comparaison avec la population. Quand on compare les prénoms de la population à ceux des élus, on peut le faire sur une base départementale : s’il y a peu de Samira en Corrèze, il y aura sans doute peu d’élues nommées Samira (même si, dans le Nord, il va naitre plus de Samira).

Dans le graphique suivant, je contrôle donc par les naissances départementales :

 
Peu de changements, là aussi. Mais quand même : si les Mohamed étaient quatre fois moins fréquents qu’attendus quand on ne prenait pas en compte les départements, ils ne sont plus que 2,5 fois moins fréquents qu’attendus.

Quatrième comparaison

Il faut donc probablement contrôler par le sexe et le département, comme je le propose ci-dessous :

 
Bof, non ? Ça ne conduit pas à une modification radicale des sur- et sous-représentations. C’est probablement parce que j’ai oublié que les élus n’avaient pas 110 ans, et qu’ils n’avaient pas 10 ans non plus.

Cinquième comparaison

Il faut donc, bien entendu, contrôler par l’année de naissance. Et cela d’autant plus que les prénoms connaissent souvent une période – plutôt courte – pendant laquelle ils sont beaucoup donnés. Si les Jeannine sont peu présentes parmi les élus, c’est parce qu’elles sont en grande partie déjà décédées.

Dans le graphique suivant, je prend donc en compte la distribution par âge de la population des élus.

 
Ah, là il y a du changement. Une bonne partie des prénoms se retrouvent à proximité du rapport d’égalité entre le nombre d’élus et le nombre attendu d’élus. Mais ne peut-on pas aussi prendre en compte le sexe et le département ?

Sixième comparaison

Oh que si : dans le dernier graphique, je montre les résultats d’un calcul prenant en compte l’année de naissance, le sexe et le département d’élection des élu·e·s :

La “boule” centrale s’est encore rétrécie : on prévoie assez bien combien il y a aura de Céline élues si l’on connaît la distribution par âge, sexe et départements de la population des élues. Il reste quelques prénoms que ces variables expliquent mal : Bertrand, Armelle, Bénédicte, Etienne, Benoît, Hugues et Hubert se retrouvent trop souvent parmi les élus. Est-ce un signe que ces prénoms sont attachés à des personnes disposant de ressources sociales plus importantes ? De l’autre côté, on trouve des prénoms symétriques : Tony, Kevin, Sabrina, Nadia, Jonathan, Jessica… que l’on devrait retrouver plus souvent chez les élus.

Et Mohamed et Karim : même en tenant compte de l’âge des élus, de leur département d’élection, de leur sexe… il y a “trop peu” de Mohamed et de Karim parmi les élus municipaux. Pour quelles raisons ? Peut-être l’utilisation d’un autre prénom au quotidien et une candidature sous un autre prénom que le prénom de naissance (comme le firent ou le font Marie-Ségolène “Ségolène” Royal, Marion-Anne “Marine” Le Pen et tant d’autres). Peut-être qu’il faudrait prendre en compte une échelle plus fine que le département ? Ou peut-être qu’on trouverait d’autres raisons si on cherchait un peu.

Notes :

1. J’ai transformé les prénoms composés : Anne-Marie est Anne, Jean-Philippe est Jean…
2. J’ai asciifié les prénoms : ils n’ont plus aucun accent ni cédilles
3. C’est un peu stupide de prendre en compte les naissances départementales pour estimer une proportion attendue, comme si les élus étaient nés là où ils sont élus
4. Et en plus, avec la fin du département de la Seine en 1968, les codages bizarres de l’Outre-Mer, je ne suis pas certain de ne pas avoir été trop rapide parfois
5. J’ai sans doute fait des erreurs, mais si vous voulez les corriger, le code est sur github

L’Insee publie maintenant en accès libre, chaque année en juin ou juillet, un « Fichier des prénoms » donnant, depuis 1900, le nombre de bébés ayant reçu tel ou tel prénom. Voici donc un petit rapport sur les prénoms (2022, pdf) à télécharger…

…Ou alors à générer vous-même, à partir du code source publié sur github : le document pdf (texte et graphique) est créé avec le logiciel R.

De 1896 à la décolonisation de Madagascar, le Journal officiel de Madagascar et dépendances rend compte de l’actualité légale d’un territoire qui est alors colonie française.
Dans ce Journal officiel il est assez régulièrement fait mention de « race ». Par exemple ici :

Source Gallica

ou encore ici

Source Gallica
Mais dans le premier extrait, il s’agit d’humains, dans le second de chevaux.
Mon nominalisme radical m’a poussé à en savoir plus. J’ai donc, grâce à l’API de Gallica, récupéré toutes les occurrences de « race(s) » dans le J.O de Madagascar. L’année 1931 manque, et c’est un petit malheur. Autour de ce mot, après avoir éliminé les mots de liaison (et, ou, mais, il…), j’ai pris une fenêtre de 50 mots avant et après. J’ai ensuite procédé à une classification thématique au moyen d’un “topic modelling“. J’ai retenu trois “topics”.

Le premier, que j’ai nommé “Production”, rassemble des extraits consacré aux races bovines, et à la production de viande. Le troisième s’intéresse à la “Reproduction” et au prix des animaux, à la fécondité. Les “métis” désignent souvent des croisements de races animales, pas les enfants de couples de colons et de Malgaches. Le deuxième “topic” concerne surtout des humains : ça parle de colonie, de province, de chef, de gouverneur, de population et d’indigènes.

Et ça évolue dans le temps : chaque extrait a une probabilité d’être affecté à un “topic” (un extrait peut être attaché à plusieurs topics), et je fais la moyenne par période de 5 ans.

Si je lis bien ce que j’ai fait, et j’ai probablement fait des erreurs ici et là, c’est le thème de la Reproduction qui émerge à partir des années 1920, en réduisant la part des extraits associés aux autres thèmes. Ce n’est pas que les « indigènes » perdent leur « race » à partir de la première guerre mondiale, mais plutôt que les réflexions agricoles prennent de l’ampleur.

La lecture plus qualitative des extraits du J.O. de Madagascar laisse percevoir la déconnexion des usages du mot «race(s)». On trouvera très peu de textes qui parlent simultanément de races d’humains et de races d’animaux. La gestion des populations humaines et celle des populations de bétail ne sont pas exactement les mêmes.

La carte ci-dessous représente la proportion des voix exprimées qui sont des votes par procuration, à Paris, par bureau de vote, pour les élections municipales, législatives et présidentielles, de 2007 à 2022.

cliquez pour agrandir
On retrouve des régularités : (1) le vote par procuration est plus fréquent en période de vacances scolaires ou de «pont» (et donc au moment des présidentielles, qui ont lieu pendant les vacances de printemps), (2) le vote par procuration est plus fréquent dans les beaux quartiers que dans la ceinture de logements sociaux situés à proximité du périphérique, et (3) le vote par procuration, lors des municipales, est plus fréquent là où le résultat de l’élection est incertain (mais ce point, je devrais le vérifier).

Si l’on calcule la fréquence moyenne, sur ces vingt scrutins, du vote par procuration, on peut tracer la carte suivante :

Comme les frontières des bureaux de vote ont changé entre 2007 et 2022, j’ai découpé Paris en petits carrés et estimé la fréquence qu’on aurait si les bureaux de vote étaient ces petits carrés.

Si la particule du nom de famille (de, du, d’ ou des) ne voulait rien dire, alors les gens à particule auraient la même distribution sociale que les gens sans particule. Monsieur Dupont et monsieur du Pont seraient équivalents.
J’ai pu montrer, dans Dupont n’est pas du Pont (Histoire & mesure, 2019), que, précisément, Dupont n’est pas du Pont.
On peut en trouver une nouvelle illustration dans ce graphique, qui présente la proportion des « parrainages » (ou « présentations ») des candidats et candidates, aux élections présidentielles, depuis 1981. Soit 41 ans, huit élections, 56 candidats, et plus de 60 700 parrainages et marrainages.

Comme on peut le constater, c’est un gradient gauche-droite qui se révèle dans la distribution des « parrainages à particule ». Statistiquement, la chose est intéressante : il y a peu d’élus à particule, environ 1%, et les parrainages sont peu nombreux (entre 500 et 2000). Il ne suffirait que de quelques parrainages à particule en plus ici ou là pour faire basculer un.e candidat.e du bas en haut de cette liste. Mais ce n’est pas ce que l’on observe…

 

Pour comprendre dans quelles recherches s’inscrit ce graphique, vous pouvez lire Dupont n’est pas du Pont.

Qui utilise son prénom dans son enseigne commerciale ?
Dans le fichier Sirene, je sélectionne les entrepreneurs individuels (au sens de « unités légales » identifiées par un nom et un prénom) et dont l’entreprise dispose d’une « enseigne commerciale », soit environ 560 000 entreprises fin 2021.
Environ 10% de ces entreprises ont, dans leur enseigne commerciale, le prénom de l’entrepreneur/entrepreneuse. Par exemple « Aux fleurs de Line » est le magasin de Line Dupont. Les femmes ont tendance à utiliser un peu plus leur prénom que les hommes, qui, eux, utilisent beaucoup plus leur nom de famille : « Maçonnerie Dupont » est l’entreprise de Maurice Dupont. Les femmes constituent environ 43% des entrepreneuses individuelles dont l’entreprise a une enseigne commerciale.
La chose amusante, du moins je la trouve amusante, c’est que dans les secteurs où les femmes sont peu fréquentes (les «travaux d’installation électrique», l’«entretien et réparation de véhicules»…), elles utilisent beaucoup moins leur prénom que les hommes. «Dupont Réparation» est la boîte de mécanique de Line Dupont, «Maurice Répare» est la boîte de mécanique de Maurice Dupont. On voit moins ça quand les hommes sont ultraminoritaires : certes ils utilisent moins leur prénom en coiffure ou «soins de beauté», mais pas autant, et on ne retrouve pas un tel coude à droite du graphique.
 

cliquez pour agrandir
 
Dans les secteurs masculins, les femmes ne mettent pas en avant leur appartenance minoritaire… ce qui fait qu’elles apparaissent encore moins présentes qu’elles ne le sont en réalité.

L’Annuaire de l’éducation, ce sont des informations sur près de 70 000 établissements scolaires et administrations diverses de l’Éducation nationale. Il est en ligne sur data.gouv.fr.
Les établissements sont géolocalisés, et on dispose de leur statut (public, privé) et du nombre d’élèves.
On peut alors tracer assez rapidement une carte, comme celle-ci :

Les proportions ne doivent pas être totalement fausses : on retrouve bien la géographie connue de l’implantation des écoles privées en France.

Les établissements scolaires ont un nom, et ces noms varient en fonction du statut.

Le tout a été réalisé avec R, et le code est sur github : 2021-annuaire-education-github.R (parce que science ouverte, données libres, partage de code).

Le Journal of Interdisciplinary History vient de publier un article (co-écrit avec Nicolas Todd, du Centre Roland Mousnier, CNRS) sur la transmission des prénoms pendant la Première Guerre mondiale.
Ce que nous avons cherché à expliquer, c’est, essentiellement, ce graphique :

Entre 1905 et le 1er août 1914, mois après mois, semaine après semaine, 12% des garçons environ reçoivent en premier prénom le premier prénom de leur père. D’après les données fournies par geneanet, c’est très stable mais à la baisse, à mesure que les parents cessent de transmettre un prénom et préfèrent, pour leurs enfants, des prénoms nouveaux. Le graphique précédent se concentre sur le taux hebdomadaire entre janvier 1913 et mars 1915, pour les garçons (on observerait la même chose pour les filles).
Mais dès la semaine du 3 août 1914, après la déclaration de guerre et la mobilisation générale du 1er août 1914, le taux de transmission passe à 17 ou 18%. On observerait des choses similaires, mais avec des proportions plus élevées, si l’on s’était intéressé à « la transmission d’un des prénoms du père à son fils » (par exemple le 3e prénom du père transmis en première position).
Toute la question est de savoir à quoi est due cette augmentation rapide ? On pourrait croire à de l’imitation, mais c’est trop rapide, le basculement se fait en quelques heures à peine, et qui donc les mères imiteraient ? Ce n’est pas non plus — en tout cas pas au cours des trois premières semaines d’août — lié aux décès des pères. Enfin ce n’est pas — à elle seule — la situation de guerre et la perturbation générale de la « division sociale du travail » qui conduit à cette hausse. Car tout redevient normal (au niveau des prénoms) en mai 1915 alors que tout reste en guerre.

Pourquoi donc, neuf mois environ après le début du conflit, ce taux de transmission revient au niveau initial ? (Indice : neuf mois).

Dans l’article, nous avançons l’idée selon laquelle la sur-transmission est liée au niveau de risque encouru par le père : ce sont les pères susceptibles de décéder dont le prénom est transmis. Ainsi les pères qui décèderont après la naissance de leur enfant, pendant la guerre, voient leur prénom plus transmis que les autres pères. Et les pères qui décèdent *avant* la naissance de leur enfant (les pères dont le risque est avéré, donc) « voient » très souvent leur prénom transmis.

On s’intéresse aussi à l’héroïsation, mais en se penchant sur la transmission du prénom des oncles. En effet, le créneau de transmission, pour les pères, est limité : leurs enfants ne peuvent naître plus de neuf mois après son décès. Ce n’est pas le cas des oncles : cinq ou six ans après leur décès, leur prénom peut toujours être transmis. Et la surtransmission du prénom des oncles décédés pendant la guerre dure longtemps, jusqu’au milieu des années vingt.

Pour en savoir plus, vous pouvez lire l’article “Naming for Kin during World War I: Baby Names as Markers for War”, mais aussi regarder la capsule vidéo sur youtube, ou consulter le code de déduplication utilisé pour cette enquête (et posté sur github). Une page spécifique consacré à “Naming for Kin” contient d’autres informations.

Maintenant que l’Institut géographique national a libéré ses données, on dispose des découpages géographiques à des échelles très fines : IRIS ou communes, par exemple.
Mais parfois, on a besoin d’un autre découpage de la France, parce que les données sont disponibles à une autre échelle, celle des ressorts des tribunaux judiciaires par exemple, ou un mélange de départements, régions, EPCI…

Commençons par les tribunaux. On trouve, sur le site de l’observatoire des territoires le tribunal de rattachement de toutes les communes françaises. On peut donc, à partir du fichier “ADMIN EXPRESS” de l’IGN, faire la jointure entre communes et tribunal, pour dessiner la carte des ressorts des 164 tribunaux.

La carte des ressorts des tribunaux :

que l’on peut relier à des données (comme la durée moyenne des affaires) :

Et maintenant le recensement. L’insee met à disposition, en accès libre, les fichiers détail du recensement. Il existe un fichier avec les individus localisés à la région, fichier proposant des variables avec des modalités très fines, comme la profession détaillée. Le titre du fichier est légèrement trompeur, car les individus sont localisés à l’échelle de la région pour les régions peu peuplées, mais aussi à l’échelle du département, pour les départements de plus de 700 000 personnes, et à l’échelle de l’EPCI (pour Paris, Marseille, Lille, Lyon, Bordeaux et Toulouse). Cela donne un découpage un peu incongru de la France, que voici :

Comme vous pouvez le constater, on trouve les départements peuplés de la Bretagne, des grosses métropoles, et de larges régions un peu plus vides.

Ce découpage n’est pas inutile. Voici, par exemple, une cartographie de la part d’immigré.e.s parmi les hommes et femmes de ménage auprès des particuliers :

Je vais essayer de mettre le code permettant de générer ces cartes sur github.