L’initiale de mon prénom a-t-elle un genre ?
Les prénoms ont un genre : Aurélia et Aurélien n’ont probablement pas été déclarés avec le même sexe. La terminaison des prénoms aussi : Clara, Léa, Zora, Anna… Sophie, Mélanie, Marie…
Mais qu’en est-il de l’initiale ?
Sur les graphiques suivant, vous trouvez en abscisses un ‘taux de masculinité’ (nombre de bébés garçons / nombre de bébé filles [merci Pierre !]) et en ordonnées le nombre total de naissances.
Pour les naissances de 2008, les prénoms en C, L, Z ou O comptent principalement des filles (2 fois plus de filles que de garçons). Les prénoms en T, G, Y, B, W, U, Q, et X sont surtout donnés aux garçons.
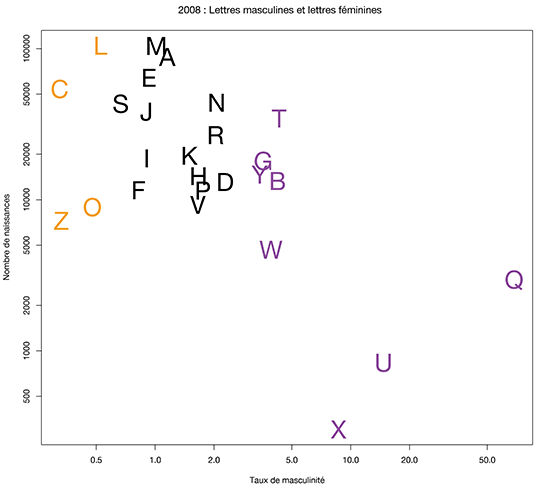
En 1970, les prénoms en Z étaient déjà féminins (ainsi que les prénoms en I, K, V et N). Mais les prénoms en L étaient autant féminins que masculins.

Il semble donc que si les initiales des prénoms sont objectivement “genrées”, l’association entre genre et initiale est instable : la terminaison marque bien plus que l’initiale le genre de la personne qui porte le prénom.
Ceci s’aperçoit bien si l’on regarde l’évolution temporelle, en fonction du “taux de masculinité” des 26 initiales disponibles en français.

Cliquez pour ouvrir l’image et pouvoir la déchiffrer [pdf]
À un moment donné, la plupart des initiales semblent bien “genrées” : mais quelques années après, l’association initiale/genre a pu s’inverser. Et les initiales qui restent constamment masculines ou féminines ne sont pas très répandues.


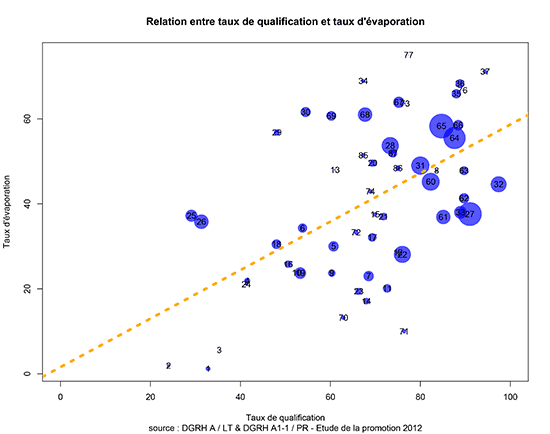









 Le “Projet mentions” vous permet d’avoir accès aux statistiques, à la répartition des notes des personnes portant le même prénom que vous, et à une comparaison des résultats du “groupe-prénom” avec la moyenne des candidats.
Le “Projet mentions” vous permet d’avoir accès aux statistiques, à la répartition des notes des personnes portant le même prénom que vous, et à une comparaison des résultats du “groupe-prénom” avec la moyenne des candidats.
 Explorez le graphe en haute résolution
Explorez le graphe en haute résolution

